Central Limit Theorem Part 2: Retaliation

Discrete population, with different probabilities associated with different numbers

Sampling distribution of means from the discrete parent population, with a sample size of n=30

In the last post, we left the central limit theorem defined as a normally-distributed sampling distribution of means reflecting the shape of the normally-distributed parent population, but with a smaller spread and less variance. However, what happens when we sample from a non-normal distribution, such as an exponential distribution or a discrete distribution?

As it turns out, the sampling distribution of means is also normal, regardless of the shape of the parent population. This holds for sample sizes of about 30 or more, which is why the central limit theorem is also sometimes referred to as the law of large numbers.

This is shown in the following video, and can be modified with this R script.

The Central Limit Theorem: Part 1

Random sample of numbers from a normal distribution, N ~ (100, 10). Actual normal distribution is superimposed in red.

One fundamental concept for hypothesis testing is something called the Central Limit Theorem. This theorem states that, for large enough sample sizes and for enough samples, we begin to build a sampling distribution that is approximately normal. More importantly, when we build sampling distributions of the means selected from a population, the average mean is identical to the mean of the parent population.

To illustrate this in R, from the parent population we can take random samples of several different sizes - 10, 50, 300 - and plot those samples as a histogram. These samples will roughly follow the shape of the population they were drawn from - in this case, the normal distribution with a mean of 100 and a standard deviation of 10 - and the more observations we have in our sample, the more closely it reflects the actual parent population. Theoretically, if our sample were large enough, it would in essence sample the entire population and therefore be the same as the population.

However, for smaller sample sizes, we can calculate the mean of each sample and then plot that value in a histogram. If we do this enough times, the mean of the sampling distribution has less spread and more tightly clusters around the mean of the parent population. Increasing the sample size does the same thing.

The demo script can be downloaded here; I have basically copied the code from this website, but distilled it into an R script that can be used and modified by anybody.

Brief Overview of Standard Error

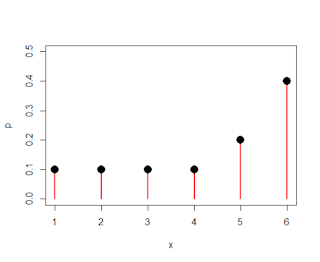
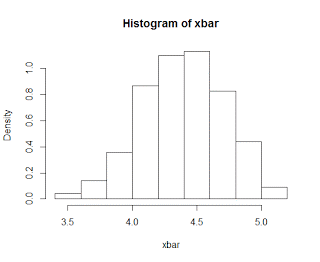
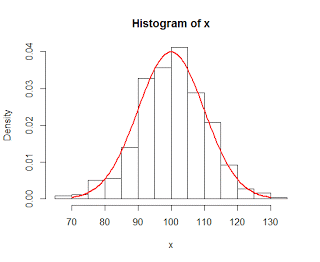
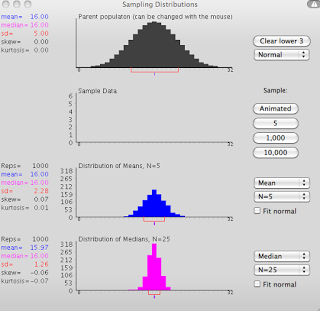
As I begin teaching a statistics course next semester, I've been spending the past couple of weeks hitting the books and refreshing my statistical knowledge; however, to my dismay, I remember virtually nothing of what was taught during my salad days of college, when my greatest concern was how fast I could run eight kilometers, and whether there would be enough ice cream left over in the Burton Dining Hall after a late workout. You laugh now, but during certain eras of one's lifetime, there are specific things that take on especial significance, only to be later ridiculed or belittled; as what is important to an adult may seem insignificant to a child, whereas what is a matter of life and death for the child may seem silly to the adult, even though there is, deep down, recognition of the same hopes and fears, the child the father of the man.

In any case, imagine my sphincter-tightening (and subsequent releasing) horror when I realized how little I actually knew, and with what haste I began to relearn the fundamentals; not only in statistics, but in several other related fields, such as biology, physics, eschatology, chemistry, and astrology, which are needed to have any sense about what one is doing when analyzing neuroimaging data. It is one thing to bandy about the usual formulas and fill them in as needed; it is completely another to learn enough jargon so that, even if you still do not understand it, you can use enough impressive-sounding words to allay any fears that you are hopelessly, utterly ignorant. And this, I maintain, is the end of all good education.

I leave you with one of the most famous quotes about the value of education, from George Washington's second inaugural address:

Power flows to the one who knows how. Desire alone is not enough.

More details about standard error can be found in the following video, which features a legit, squeaking chalkboard.

Super Useful Sampling Distributions Applet

Similar to the applets I used for my P211 research methods class, there is an online program which allows the user to specify a population distribution, and then build a sampling distribution of statistics such as mean, median, and variance. When I was first starting out I had a difficult time grasping what exactly a sampling distribution was, or what it meant, exactly; but tools like this are great for visualizing the process and building an intuition about what's really going on. The result is, I still don't understand it - like, at all - but I sure as hell feel more confident. And that's what is really important.