Automating SPM Contrasts

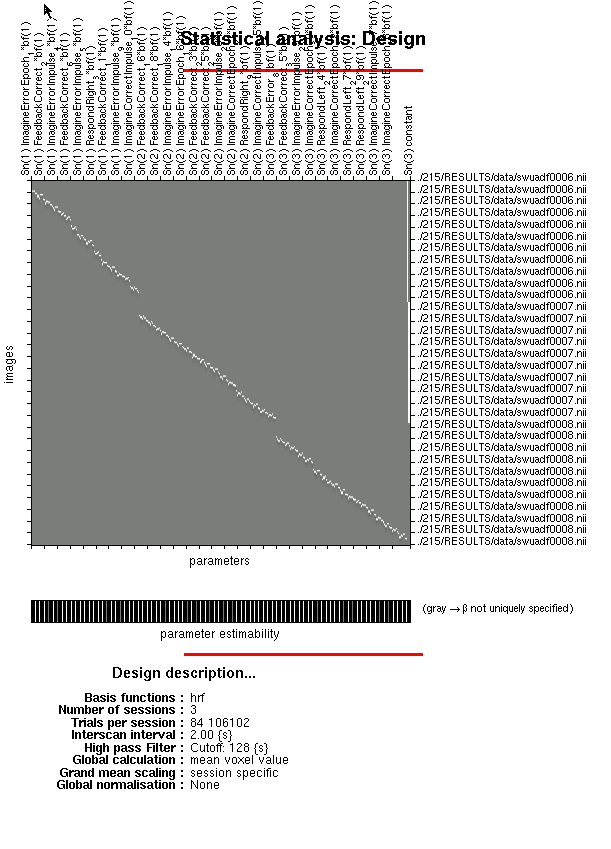
Manually typing in contrasts in SPM is a grueling process that can have a wide array of unpleasant side effects, including diplopia, lumbago, carpal tunnel syndrome, psychosis, violent auditory and visual hallucinations, hives, and dry mouth. These symptoms are only compounded by the number of regressors in your model, and the number of subjects in your study.

Fortunately, there is a simply way to automate all of this - provided that each subject has the same number of runs, and that the regressors in each run are structured the same way. If they are, though, the following approach will work.

First, open up SPM and click on the TASKS button in the upper right corner of the Graphics window. The button is marked "TASKS" in capital letters, because they really, really want you to use this thing, and mitigate all of the damage and harm in your life caused by doing things manually. You then select the Stats menu, then Contrast Manager. The options from there are straightforward, similar to what you would do when opening up the Results section from the GUI and typing in contrasts manually.

When specifying the contrast vector, take note of how many runs there are per subject. This is because we want to take the average parameter estimate for each regressor we are considering; one can imagine a scenario where one of the regressors occurs in every run, but the other regressor only happens in a subset of runs, and this more or less puts them on equal footing. In addition, comparing the average parameter or contrast estimate across subjects is easier to interpret.

Once you have the settings to your satisfaction, save it out as a .mat file - for example, 'RunContrasts.mat'. This can then be loaded from the command line:

load('RunContrasts')

Which will put a structure called "jobs" in your workspace, which contains all of the code needed to run a first-level contrast. The only part of it we need to change when looping over subjects is the spmmat field, which can be done with code like the following:

subjList=[207 208]; %And so on, including however many subjects you want

for subj=subjList

    jobs{1}.stats{1}.con.spmmat =     {['/data/hammer/space4/MultiOutcome2/fmri/' num2str(subj) '/RESULTS/model_multiSess/SPM.mat']} %This could be modified so that the path is a variable reflecting where you put your SPM.mat file
    spm_jobman('run', jobs)

end

This is demonstrated in the following pair of videos; the first, showing the general setup, and the second showing the execution from the command line.

Updated SPM Command Line, Including Beta Series Option

I've updated the code of the previously discussed previous script in the previous post, previously, including the addition of more help text to explain certain options and termination of the script if the timing file is not found.

However, the biggest change is a block of code to convert the timings files so that each trial is now a regressor, before entering them into the GLM. With so many regressors, the GLM will look a little funky; possibly something like this:

Note that, since there are so many regressors and so many scans, not all of them are going to be labeled individually; but it should look as though there is only one estimation per column, or blip of white underneath each regressor. Also due to space constraints the parameter estimability may not be completely visible, but when each trial is being estimated individually, you should still get a beta for each trial. Check the output directory to make sure that you have the number of betas you think you should have: one for each trial, plus the amount of session constants (usually equal to the number of runs for the subject).

The updated script can be found here; as always, send me any comments if you encounter any serious issues or bugs. I recommend using it as a replacement for the previously discussed previous script, since it can either estimate each trial individually or average them together, depending on whether you set the DO_BETASERIES flag to 1 or 0.

All of this is explained clearly in the following video:

The Central Limit Theorem: Part 1

Random sample of numbers from a normal distribution, N ~ (100, 10). Actual normal distribution is superimposed in red.

One fundamental concept for hypothesis testing is something called the Central Limit Theorem. This theorem states that, for large enough sample sizes and for enough samples, we begin to build a sampling distribution that is approximately normal. More importantly, when we build sampling distributions of the means selected from a population, the average mean is identical to the mean of the parent population.

To illustrate this in R, from the parent population we can take random samples of several different sizes - 10, 50, 300 - and plot those samples as a histogram. These samples will roughly follow the shape of the population they were drawn from - in this case, the normal distribution with a mean of 100 and a standard deviation of 10 - and the more observations we have in our sample, the more closely it reflects the actual parent population. Theoretically, if our sample were large enough, it would in essence sample the entire population and therefore be the same as the population.

However, for smaller sample sizes, we can calculate the mean of each sample and then plot that value in a histogram. If we do this enough times, the mean of the sampling distribution has less spread and more tightly clusters around the mean of the parent population. Increasing the sample size does the same thing.

The demo script can be downloaded here; I have basically copied the code from this website, but distilled it into an R script that can be used and modified by anybody.