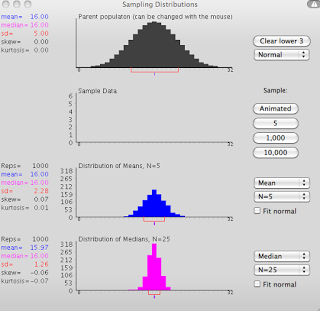
Similar to the applets I used for my P211 research methods class, there is an online program which allows the user to specify a population distribution, and then build a sampling distribution of statistics such as mean, median, and variance. When I was first starting out I had a difficult time grasping what exactly a sampling distribution was, or what it meant, exactly; but tools like this are great for visualizing the process and building an intuition about what's really going on. The result is, I still don't understand it - like, at all - but I sure as hell feel more confident. And that's what is really important.
Super Useful Sampling Distributions Applet
Similar to the applets I used for my P211 research methods class, there is an online program which allows the user to specify a population distribution, and then build a sampling distribution of statistics such as mean, median, and variance. When I was first starting out I had a difficult time grasping what exactly a sampling distribution was, or what it meant, exactly; but tools like this are great for visualizing the process and building an intuition about what's really going on. The result is, I still don't understand it - like, at all - but I sure as hell feel more confident. And that's what is really important.