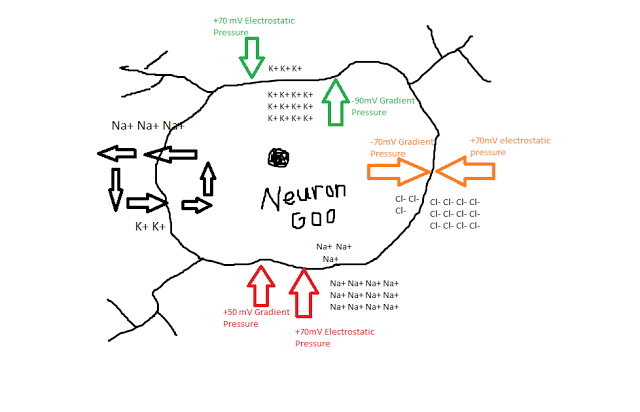
Someone very near and dear to me just sent me a picture of herself cuddled up on the couch in her pajamas with an Argentinian Tegu. That's right lady, I said Tegu. The second coming of Sodom and Gomorrah - you heard it here first, folks! I mean, I know it's the twenty-first century and all, but what the heck.
Looks like I'll be pushing her to buy that lucrative life insurance policy much earlier than planned!
Anyway, I think that little paroxysm of righteous anger provides an appropriate transition into our discussion of reinforcement learning. Previously we talked about how a simple model can simulate an organism processing a stimulus, such as a tone, and begin to associate that with rewards or lack of rewards, which in turn leads to either greater levels of dopamine firing, or depressed levels of dopamine firing. Over time, dopamine firing begins to respond to the conditioned stimulus itself instead of the reward as it becomes more tightly linked to receiving the reward in the near future. This phenomenon is so strong and reliable across all species, it can even be observed in the humble sea slug Aplysia, which is one ugly sucker if I've ever seen one. Probably wouldn't stop her from cuddling up with that monstrosity, though!
Anyway, that only describes one form of learning - to wit, classical conditioning. (Do you think I am putting on airs when I use a phrase like "to wit"? She thinks that I do; but then again, she also has passionate, perverted predilections for cold-blooded wildlife.) Obviously, any animal in the food chain - even the ones she associates with - can be classically conditioned to almost anything. Much more interesting is operant conditioning, in which an individual has to make certain choices, or actions, and then evaluate the consequences of those choices. Kind of like hugging reptiles! Oh hey, she probably thinks, let's see if hugging this lizard - this pebbly-skinned, fork-tongued, unblinking beast - results in some kind of reward, like gold coins shooting out of my mouth. In operant conditioning parlance, the rush of gold coins flowing out of one's orifice would be a reinforcer, which increases the probability of that action in the future; while a negative event, such as being fatally bitten by the reptile - which pretty much any sane person would expect to happen - would be a punisher, which decreases the probability of that action in the future.
The classically conditioned responses, in other words, serve the function of a critic which monitors for stimuli and reliably-predicted reinforcers or punishers following those stimuli, while operant conditioning can be thought of as an actor role, where choices are made and the results evaluated against what was expected. Sutton and Barto, a pair of researchers considerably less sanguinary than Hodgkin and Huxley, were among the first to propose and refine this model, assigning the critic role to the ventral striatum and the actor role to the dorsal striatum. So, that's where they are; if you want to find the actor component of reinforcement learning, for example, just grab a flashlight and examine the dorsal striatum inside someone's skull, and, hey presto! there it is. I won't tell you what it looks like.
However, we can form some abstract idea about what the actor component looks like by simulating it in Matlab. No, just in case you were wondering, this won't help you hook up with Komodo Dragons! It will, however, refine our understanding of how reinforcement learning works, by building upon the classical conditioning architecture we discussed previously. In this case, weights are still updated, but now we have two actions to choose from, which results in four combinations: either one or the other, both at the same time, or neither. In this example, only doing action 1 will lead to a reward, and this gets learned right quick by the simulation. As before, a surface map of delta shows the reward signal being transferred from the actual reward itself to the action associated with that reward, and a plot of the vectors shows action 1 clearly dominating over action 2. The following code will help you visualize these plots, and see how tweaking parameters such as the discount factor and learning rate affect delta and the action weights. But it won't help you get those gold coins, will it?
clear
clc
close all
numTrials = 200;
numSteps = 100;
weights = zeros(100,200); %Array of weights from steps 1-100, initialized to zero
discFactor = 0.995; %Discounting factor
learnRate = 0.3; %Learning Rate
delta = zeros(100,200); %Empty vector
V = []; %Empty vector
x = [zeros(1,19) ones(1,81)];
r = zeros(100,200); %Reward vector, which will be populated with 1's whenever a reward occurs (in this case, when action1 == 1 and action2 == 0)
W1=0;
W2=0;
a1=zeros(1,numTrials);
a2=zeros(1,numTrials);
for idx = 1:numTrials
for t = 1:numSteps-1
if t==20
as1=x(t)*W1; %Compute action signals at time step 20 within each trial
as2=x(t)*W2;
ap1 = exp(as1)/(exp(as1)+exp(as2)); %Softmax function to calculate probability associated with each action
ap2 = exp(as2)/(exp(as1)+exp(as2));
n=rand;
if n<(idx)=1;
end
n=rand;
if n<ap2 a2(idx)=1;
end
if a1(idx)==1 && a2(idx)==0 %Only deliver reward when action1 ==1 and action2 ==0
r(50:55,idx)=1;
end
end
V(t,idx) = x(t).*weights(t, idx);
V(t+1,idx) = x(t+1).*weights(t+1, idx);
delta(t+1,idx) = r(t+1,idx) + discFactor.*V(t+1,idx) - V(t,idx);
weights(t, idx+1) = weights(t, idx)+learnRate.*x(t).*delta(t+1,idx);
W1 = W1 + learnRate*delta(t+1,idx)*a1(idx);
W2 = W2 + learnRate*delta(t+1,idx)*a2(idx);
end
w1Vect(idx) = W1;
w2Vect(idx) = W2;
end
figure
set(gcf, 'renderer', 'zbuffer') %Can prevent crashes associated with surf command
surf(delta)
figure
hold on
plot(w1Vect)
plot(w2Vect, 'r')


Oh, and one more thing that gets my running tights in a twist - people who don't like Bach. Who the Heiligenstadt Testament doesn't like Bach? Philistines, pederasts, and pompous, nattering, Miley Cyrus-cunnilating nitwits, that's who! I get the impression that most people have this image of Bach as some bewigged fogey dithering around in a musty church somewhere improvising fugues on an organ, when in fact he wrote some of the most hot-blooded, sphincter-tightening, spiritually liberating music ever composed. He was also, clearly, one of the godfathers of modern metal; listen, for example, to the guitar riffs starting at 6:38.
...Now excuse me while I clean up some of the coins off the floor...
Looks like I'll be pushing her to buy that lucrative life insurance policy much earlier than planned!
Anyway, I think that little paroxysm of righteous anger provides an appropriate transition into our discussion of reinforcement learning. Previously we talked about how a simple model can simulate an organism processing a stimulus, such as a tone, and begin to associate that with rewards or lack of rewards, which in turn leads to either greater levels of dopamine firing, or depressed levels of dopamine firing. Over time, dopamine firing begins to respond to the conditioned stimulus itself instead of the reward as it becomes more tightly linked to receiving the reward in the near future. This phenomenon is so strong and reliable across all species, it can even be observed in the humble sea slug Aplysia, which is one ugly sucker if I've ever seen one. Probably wouldn't stop her from cuddling up with that monstrosity, though!
Anyway, that only describes one form of learning - to wit, classical conditioning. (Do you think I am putting on airs when I use a phrase like "to wit"? She thinks that I do; but then again, she also has passionate, perverted predilections for cold-blooded wildlife.) Obviously, any animal in the food chain - even the ones she associates with - can be classically conditioned to almost anything. Much more interesting is operant conditioning, in which an individual has to make certain choices, or actions, and then evaluate the consequences of those choices. Kind of like hugging reptiles! Oh hey, she probably thinks, let's see if hugging this lizard - this pebbly-skinned, fork-tongued, unblinking beast - results in some kind of reward, like gold coins shooting out of my mouth. In operant conditioning parlance, the rush of gold coins flowing out of one's orifice would be a reinforcer, which increases the probability of that action in the future; while a negative event, such as being fatally bitten by the reptile - which pretty much any sane person would expect to happen - would be a punisher, which decreases the probability of that action in the future.
The classically conditioned responses, in other words, serve the function of a critic which monitors for stimuli and reliably-predicted reinforcers or punishers following those stimuli, while operant conditioning can be thought of as an actor role, where choices are made and the results evaluated against what was expected. Sutton and Barto, a pair of researchers considerably less sanguinary than Hodgkin and Huxley, were among the first to propose and refine this model, assigning the critic role to the ventral striatum and the actor role to the dorsal striatum. So, that's where they are; if you want to find the actor component of reinforcement learning, for example, just grab a flashlight and examine the dorsal striatum inside someone's skull, and, hey presto! there it is. I won't tell you what it looks like.
However, we can form some abstract idea about what the actor component looks like by simulating it in Matlab. No, just in case you were wondering, this won't help you hook up with Komodo Dragons! It will, however, refine our understanding of how reinforcement learning works, by building upon the classical conditioning architecture we discussed previously. In this case, weights are still updated, but now we have two actions to choose from, which results in four combinations: either one or the other, both at the same time, or neither. In this example, only doing action 1 will lead to a reward, and this gets learned right quick by the simulation. As before, a surface map of delta shows the reward signal being transferred from the actual reward itself to the action associated with that reward, and a plot of the vectors shows action 1 clearly dominating over action 2. The following code will help you visualize these plots, and see how tweaking parameters such as the discount factor and learning rate affect delta and the action weights. But it won't help you get those gold coins, will it?
clear
clc
close all
numTrials = 200;
numSteps = 100;
weights = zeros(100,200); %Array of weights from steps 1-100, initialized to zero
discFactor = 0.995; %Discounting factor
learnRate = 0.3; %Learning Rate
delta = zeros(100,200); %Empty vector
V = []; %Empty vector
x = [zeros(1,19) ones(1,81)];
r = zeros(100,200); %Reward vector, which will be populated with 1's whenever a reward occurs (in this case, when action1 == 1 and action2 == 0)
W1=0;
W2=0;
a1=zeros(1,numTrials);
a2=zeros(1,numTrials);
for idx = 1:numTrials
for t = 1:numSteps-1
if t==20
as1=x(t)*W1; %Compute action signals at time step 20 within each trial
as2=x(t)*W2;
ap1 = exp(as1)/(exp(as1)+exp(as2)); %Softmax function to calculate probability associated with each action
ap2 = exp(as2)/(exp(as1)+exp(as2));
n=rand;
if n<(idx)=1;
end
n=rand;
if n<ap2 a2(idx)=1;
end
if a1(idx)==1 && a2(idx)==0 %Only deliver reward when action1 ==1 and action2 ==0
r(50:55,idx)=1;
end
end
V(t,idx) = x(t).*weights(t, idx);
V(t+1,idx) = x(t+1).*weights(t+1, idx);
delta(t+1,idx) = r(t+1,idx) + discFactor.*V(t+1,idx) - V(t,idx);
weights(t, idx+1) = weights(t, idx)+learnRate.*x(t).*delta(t+1,idx);
W1 = W1 + learnRate*delta(t+1,idx)*a1(idx);
W2 = W2 + learnRate*delta(t+1,idx)*a2(idx);
end
w1Vect(idx) = W1;
w2Vect(idx) = W2;
end
figure
set(gcf, 'renderer', 'zbuffer') %Can prevent crashes associated with surf command
surf(delta)
figure
hold on
plot(w1Vect)
plot(w2Vect, 'r')
======================
Oh, and one more thing that gets my running tights in a twist - people who don't like Bach. Who the Heiligenstadt Testament doesn't like Bach? Philistines, pederasts, and pompous, nattering, Miley Cyrus-cunnilating nitwits, that's who! I get the impression that most people have this image of Bach as some bewigged fogey dithering around in a musty church somewhere improvising fugues on an organ, when in fact he wrote some of the most hot-blooded, sphincter-tightening, spiritually liberating music ever composed. He was also, clearly, one of the godfathers of modern metal; listen, for example, to the guitar riffs starting at 6:38.
...Now excuse me while I clean up some of the coins off the floor...