For regional homogeneity analysis (ReHo), many of the processing steps of FMRI data remain the same: slice-timing correction, coregistration, normalization, and many of the other steps are identical to traditional resting-state analyses. However, the order of the steps can be changed, depending on whatever suits your taste; as with many analysis pipelines, there is no single correct way of doing it, although some ways are more correct than others.
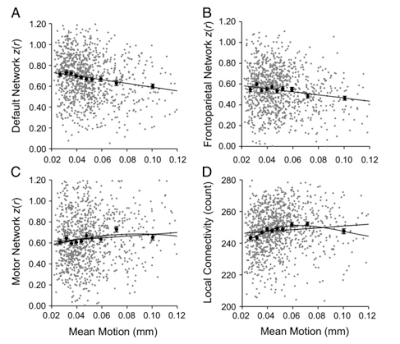
One of the most comprehensive overviews of ReHo processing was done by Maximo et al (2013), where datasets were processed using different types of signal normalization, density analysis, and global signal regression. I don't know what any of those terms mean, but I did understand when they tested how smoothness affected the ReHo results. As ReHo looks at local connectivity within small neighborhoods, spatial smoothing can potentially inflate these correlation statistics by averaging signal together over a large area and artificially increasing the local homogeneity of the signal. Thus, smoothing is typically done after ReHo is applied, although some researchers eschew it altogether.
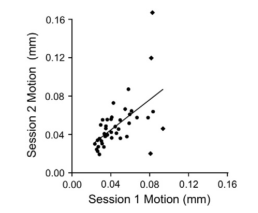
So, should you smooth? Consider that each functional image already has some smoothness added to it when it comes directly off the scanner, and also that any transformation or movement of the images introduces spatial interpolation as well. Further, not all of this interpolations and inherent smoothness will be exactly the same for each subject. Given this, it makes the most sense to smooth after ReHo has been applied, but also to use a tool such as AFNI's 3dFWHMx to smooth each image to the same level of smoothness; however, if that still doesn't sit well with you, note that the researcher's from the abovementioned paper tried processing pipelines both with and without a smoothing step, and found almost identical results for each analysis stream.
Taken together, most of the steps we used for processing our earlier functional connectivity data are still valid when applied to a ReHo analysis; we still do the basic preprocessing steps, and still run 3dDeconvolve and 3dSynthesize commands to remove confounding motion effects from our data. However, we will only do smoothing after all of these commands have been run, and use 3dFWHMx to do it instead of 3dmerge.
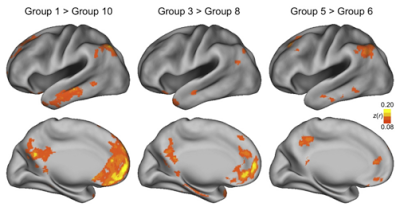
One last consideration is the neighborhood you will use for ReHo. As a local connectivity measure, we can specify how much of the neighborhood we want to test for correlation with each voxel; and the most typical options are using immediate neighbors of 7, 19, or 27 voxels, which can be specified in the 3dReHo command with the -nneigh option. "7" will mean to consider only those neighboring voxels with one face touching; "19" will calculate the time-series correlation with any voxel touching with a face or an edge (e.g., a straight line bordering the current voxel); and "27" will do the analysis for any voxel with an abutting face, edge, or corner (think of it as the test voxel in the center of a Rubik's cube, and that voxel being correlated with every other voxel in the cube).
In the next part, we will go over some important rhetorical questions, along with a video showing how the command is done.
One of the most comprehensive overviews of ReHo processing was done by Maximo et al (2013), where datasets were processed using different types of signal normalization, density analysis, and global signal regression. I don't know what any of those terms mean, but I did understand when they tested how smoothness affected the ReHo results. As ReHo looks at local connectivity within small neighborhoods, spatial smoothing can potentially inflate these correlation statistics by averaging signal together over a large area and artificially increasing the local homogeneity of the signal. Thus, smoothing is typically done after ReHo is applied, although some researchers eschew it altogether.
So, should you smooth? Consider that each functional image already has some smoothness added to it when it comes directly off the scanner, and also that any transformation or movement of the images introduces spatial interpolation as well. Further, not all of this interpolations and inherent smoothness will be exactly the same for each subject. Given this, it makes the most sense to smooth after ReHo has been applied, but also to use a tool such as AFNI's 3dFWHMx to smooth each image to the same level of smoothness; however, if that still doesn't sit well with you, note that the researcher's from the abovementioned paper tried processing pipelines both with and without a smoothing step, and found almost identical results for each analysis stream.
Taken together, most of the steps we used for processing our earlier functional connectivity data are still valid when applied to a ReHo analysis; we still do the basic preprocessing steps, and still run 3dDeconvolve and 3dSynthesize commands to remove confounding motion effects from our data. However, we will only do smoothing after all of these commands have been run, and use 3dFWHMx to do it instead of 3dmerge.
One last consideration is the neighborhood you will use for ReHo. As a local connectivity measure, we can specify how much of the neighborhood we want to test for correlation with each voxel; and the most typical options are using immediate neighbors of 7, 19, or 27 voxels, which can be specified in the 3dReHo command with the -nneigh option. "7" will mean to consider only those neighboring voxels with one face touching; "19" will calculate the time-series correlation with any voxel touching with a face or an edge (e.g., a straight line bordering the current voxel); and "27" will do the analysis for any voxel with an abutting face, edge, or corner (think of it as the test voxel in the center of a Rubik's cube, and that voxel being correlated with every other voxel in the cube).
In the next part, we will go over some important rhetorical questions, along with a video showing how the command is done.