Andy's Brain Blog

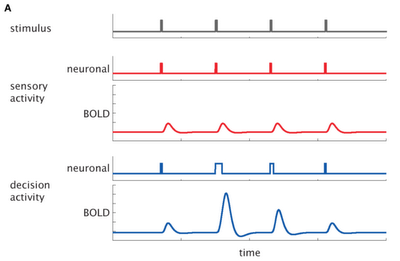
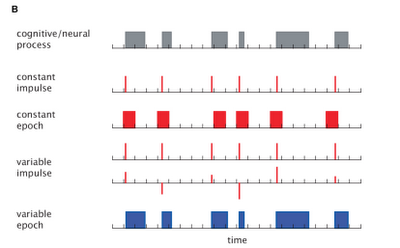
Those who are the youngest children in the family are keenly aware of the disadvantages of being last in the pecking order; the quality of toys, clothes, and nutrition is often best for the eldest children in the family, and gradually tapers off as you reach the last kids, who are usually left with what are called, in parent euphemisms, "hand-me-downs."

In reality, these are things that should have been discarded several years ago due to being broken, unsafe, containing asbestos, or clearly being overused, such as pairs of underwear that have several holes in them so large that you're unsure of where exactly your legs go.

In SPM land, a similar thing happens to parametric modulators, with later modulators getting the dregs of the variance not wanted by the first modulators. Think of variance as toys and cake, and parametric modulators as children; everybody wants the most variance, but only the first modulators get the lion's share of it; the last modulators get whatever wasn't given to the first modulators.

The reason this happens is because when GLMs are set up, SPM uses a command, spm_orth, to orthogonalize the modulators. The first modulator is essentially untouched, but all other modulators coming after it are orthogonalized with respect to the first; and this proceeds in a stepwise function, with the second modulator getting whatever was unassigned to the first, the third getting whatever was unassigned to the second, and so on.

(You can see this for yourself by doing a couple of quick simulations in Matlab. Type x1=rand(10,1), and x2=rand(10,1), and then combine the two into a matrix with xMat = [x1 x2]. Type spm_orth(xMat), and notice that the first column is unchanged, while the second is greatly altered. You can then flip it around by creating another matrix, xMatRev = [x2 x1], and using spm_orth again to see what effect this change has.)

Be aware of this, as this can dramatically alter your results depending on how your modulators were ordered. (If they were completely orthogonal by design, then the spm_orth command should have virtually no impact; but this scenario is rare.) This came to my attention when looking at a contrast of a parametric modulator, which was one of three assigned to a main regressor. In one GLM, the modulator was last, and correspondingly explained almost no variance in the data; while in another GLM, the modulator was first, and loaded on much more of the brain. The following two figures show the difference, using exactly the same contrast and correction threshold, but simply reversing the order of the modulators:

Results window when parametric modulator was the last one in order.

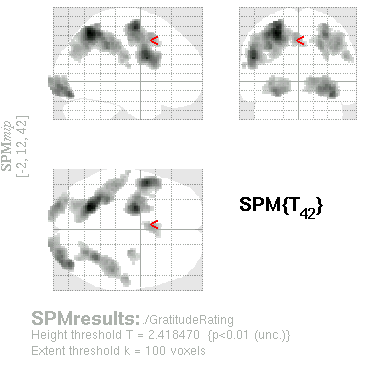Results window when parametric modulator was the first one in order.

This can be dealt with in a couple of ways:

Comment out the spm_orth call in two scripts used in setting up the GLM: line 229 in spm_get_ons.m, and lines 285-287 in spm_fMRI_design.m. However, this might affect people who actually do want the orthogonalization on, and also this increases the probability that you will screw something up. Also note that doing this means that the modulators will not get de-meaned when entered into the GLM.
Create your own modulators by de-meaning the regressor, inserting your value at the TR where the modulator occurred, then convolving this with an HRF (usually the one in SPM.xBF.bf). If needed, downsample the output to match the original TR.

It is well to be aware of all this, not only for your own contrasts, but to see how this is done in other papers. I recall reading one a long time ago - I can't remember the name - where several different models were used, in particular different models where the modulators were entered in different orders. Not surprisingly, the results were vastly different, although why this was the case wasn't clearly explained. Just something to keep in mind, as both a reader and a reviewer.

I should also point out that this orthogonalization does not occur in AFNI; the order of modulators has no influence on how they are estimated. A couple of simulations should help illustrate this:

Design matrices from AFNI with simulated data (one regressor, two parametric modulators.) Left: PM1 entered first, PM2 second. Right: Order reversed. The values are the same in both windows, just transposed to illustrate which one was first in the model.

More information on the topic can be found here, and detailed instructions on how to construct your own modulators can be found on Tor Wager's lab website.

This subject was brought to my attention by a colleague who wanted to know whether parametric modulation or duration modulation was a better way to account for RT effects. While it can depend on the question you are trying to answer, often duration modulation (referred to here as a "variable epoch model") works best. The following highlights the different approaches for modeling trials which involve a period of decision-making or an interval between presentation of a stimulus and the resulting response.

Over the past few years there has been a renewed interest in modeling duration in fMRI data. In particular, a methods paper by Grinband and colleagues (2008) compared the effects of modeling the duration of a trial - as measured by its reaction time (RT) - against models which used RT as a parametric modulator and against models which did not use RT at all. The argument against using RT-modulated regressors was that, at short time intervals (i.e., less than four seconds), using an impulse function was a good approximation to the resulting BOLD signal (cf. Henson, 2003).

Figure depicting relationship between stimulus onset, BOLD response, and underlying neural activity. Red lines: activity associated with punctate responses (e.g., light flashed at the subject). Blue lines: Activity associated with trials of unequal duration (e.g., decision-making).

However, for a few investigators, such assumptions were not good enough. To see whether different models of RT led to noticeable differences in BOLD signal, Grinband et al (2008) examined four types of modeling:

Convolving the onset of a condition or response with the canonical HRF (constant impulse model);
Separately modeling both the main effect of the condition as well as a mean-centered parametric modulator - in this case RT (variable impulse model);
Binning each condition onset into a constant amount of time (e.g., 2 seconds) and convolving with the canonical HRF (constant epoch model); and
Modeling each event as a boxcar function equal to the length of the subject's RT (variable epoch model).

Graphical summary of models from Grinband et al (2008). Top: Duration of cognitive process as indexed by reaction time. Constant Impulse: Onset of each event treated as a punctate response. Constant Epoch: Onset of each event convolved with boxcar function of constant duration. Variable Impulse: Punctate response functions modulated by mean-centered parameter (here, RT). Variable Epoch: Each event modeled by boxcar of duration equal to that event's RT.

Each of these models was then compared using data from a decision-making task in which subjects determined whether a line was long or short. If this sounds uninteresting to you, you have obviously never done a psychology experiment before.

The authors found that the variable epoch model - in other words, convolving each event with a boxcar equal to the length of the subject's RT for that trial - captured more of the variability in the BOLD response, in addition to reducing false positives as compared to the other models. The variable epoch model also dramatically increased sexual drive and led to an unslakeable thirst for mindless violence. Therefore, these simulations suggest that for tasks requiring time - such as decision-making tasks - convolution with boxcar regressors is a more faithful representation of the underlying neuronal dynamics (cf. the drift-diffusion model of Ratcliff & McKoon, 2008). The following figures highlight the differences between the impulse and epoch models:

Comparison of impulse models and epoch models as depicted in Grinband et al (2008). A) For impulse models, the shape remains constant while the amplitude varies; for epoch models, increasing the duration of a trial leads to changes in both shape and amplitude. B) Under the impulse model, increasing the duration of a stimulus or cognitive process (as measured by RT) leads to a reduction in explained variance.

Figure from Grinband et al (2008) showing differential effects of stimulus intensity and stimulus duration. Left: Increasing stimulus intensity has no effect on the time to peak of the BOLD response. Right: Increasing stimulus duration (or the duration of the cognitive process) leads to a linear increase in the time for the BOLD response to peak.

One caveat: note well that both parametric modulation and convolution with boxcar functions will account for RT-related effects in your data; and although the Grinband simulations establish the supremacy of boxcar functions, there may be occasions that warrant parametric modulation. For example, one may be interested in the differences of RT modulation for certain trial types as compared to others; and the regressors generated by parametric modulation will allow the researcher to test them against each other directly.