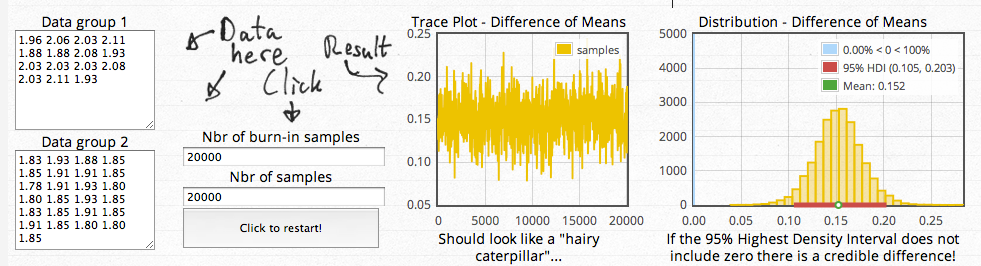
For those still struggling to understand the concepts of Bayesian inference - in other words, all of you - there is a web app developed by Rasmus Baath which allows one to see the process unfolding in real time. Similar to an independent-samples t-test, we are trying to estimate a parameter of the mean difference between the populations that the samples were drawn from; however, the Bayesian approach offers much richer information about a distribution of parameter values, and, more importantly, which ones are more credible than others, given the data that has been collected.
The web app is simple to use: You input data values for your two groups, specify the number of samples and burn-in samples (although the defaults for this are fine), and then hit the Start button. The MCMC chain begins sampling the posterior distribution, which builds up a distribution of credible parameter values, and 95% of the distribution containing the parameter values with the most credibility is labeled as the highest density interval, or HDI. This same procedure is applied to all of the other parameters informed by the data, including normality, effect size, and individual group means and standard deviations, which provides a much richer set of information than null hypothesis significance testing (NHST).
Because of this I plan to start incorporating more Bayesian statistics into my posts, and also because I believe it will overtake, replace, and destroy NHST as the dominant statistical method in the next ten years, burning its crops, sowing salt in its fields, looting its stores, stampeding its women, and ravishing its cattle. All of this, coming from someone slated to teach the traditional NHST approach next semester; which, understandably, has me conflicted. On the one hand, I feel pressured to do to whatever is most popular at the moment; but on the other, I am an opportunistic coward.
In any case, Bayesian inference is becoming a more tractable technique, thanks to programs that interface with the statistics package R, such such JAGS. Using this to estimate parameters for region of interest data, I think, will be a good first step for introducing Bayesian methods to neuroimagers.