One question I frequently hear - besides "Why are you staring at me like that?" - is, "Should I optimize my experimental design?" This question is foolish. As well ask man what he thinks of Nutella. Optimal experimental designs are essential to consider before creating an experiment, in order to ensure that there is a balance between the number of trials, the duration of the experiment, and the estimation efficiency. Optseq is one such tool which allows the experimenter to maximize all three.
Optseq, a tool developed by the good people over at MGH, helps the user order the presentation of experimental conditions or stimuli in order to optimize the estimation of beta weights for a given condition or a given contrast. By providing a list of the experimental conditions, the length of the experiment, the TR, and how long and how frequent the experimental conditions last, optseq will generate schedules of stimuli presentation that maximizes the power of the design, both through reducing variance due to noise and increasing the efficiency of estimating beta weights. This is especially important in event-related designs, which are discussed in greater detail below.
Chapter 1: Slow Event-Related Designs
Slow event-related designs refer to experimental paradigms in which the hemodynamic response function (HRF) for a given condition does not overlap with another condition's HRF. For example, let us say that we have an experiment in which IAPS photos are presented to the subject at certain intervals. Let us also say that there are three classes of photos (or conditions): 1) Disgusting pictures (DisgustingPic); 2) Attractive pictures (AttractivePic); and neutral pictures (NeutralPic). The order in which these pictures are presented will be at a long enough time interval so that the HRFs do not overlap, as shown in the following figure (Note: All of the following figures are taken from the AFNI website; all credit and honor is theirs. They may find these later and try to sue me, but that is a risk I am willing to take):
The interstimulus time interval (ITI) in this example is 15 seconds, allowing enough time for the entire HRF to rise and decay, and therefore allow the experimenter to estimate a beta weight for each condition individually without worrying about overlap in the HRFs. (The typical duration of an HRF, from onset to decay back to baseline, is roughly 12 seconds, with a long period of undershoot and recovery thereafter). However, slow event-related designs suffer from relatively long experimental durations, since the time after each stimulus presentation has to allow enough time for the HRF to decay to baseline levels of activity. Furthermore, the subject may become bored after such lengthy "null" periods, and may develop strategies (aka, "sets") when the timing is too predictable. Therefore, quicker stimulus presentation is desirable, even if it leads to overlap in the conditions's HRFs.
Chapter 2: Rapid (or Fast) Event-Related Designs
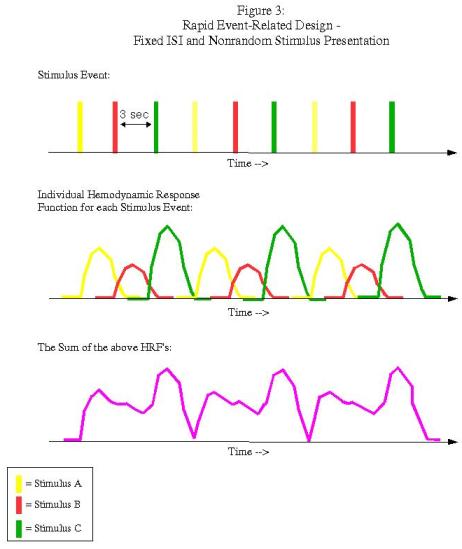
Rapid event-related designs refer to experimental paradigms in which the ISI between conditions is short enough so that the hemodynamic response function (HRF) for a given condition overlaps with another condition's HRF. Theoretically, given the assumption of linearity of overlapping HRFs, this shouldn't be a problem, and the contribution of each condition's HRF can be determined through a process known as deconvolution. However, this can be an issue when the ISI's are fixed and the presentation of stimuli is fixed as well:
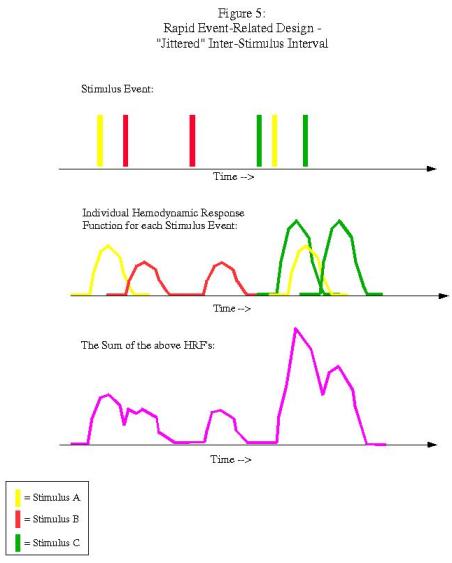
In this example, each condition follows the other in a fixed pattern: A followed by B followed by C. However, the resulting signal arising from the combination of HRFs (shown in purple in the bottom graph) is impossible to disentangle; we have no way of knowing, at any given time point, what amount of the signal is due to condition A, B, or C. In order to resolve this, we must randomize the presentation of the stimuli and also the duration of the ISI's (a process known as "jittering"):
Now we have enough variability so that we can deconvolve the contribution of each condition to the overall signal, and estimate a beta weight for each condition. This is the type of experimental design that optseq deals with.
Chapter 3: Optseq
In order to use optseq, first download the software from the MGH website (or, just google "optseq" and click on the first hit that comes up). Put the shell script into a folder somewhere in your path (such as ~/abin, if you have already downloaded AFNI) so that it will execute from anywhere within the shell. After you have done this you may also want to type "rehash" at the command line in order to update the paths. Then, type "optseq2" to test whether the program executes or not (if it does, you should get the help output, which is generated when no argument are given).
Optseq needs four pieces of information: 1) The number of time points in a block of your experiment; 2) The TR; 3) A permissible range of the minimum and maximum amounts of time after presentation of a stimulus and the start of the next (aka, the post-stimulus delay, or PSD); and 4) How many conditions there are in your experiment, as well as how long they are per trial and how many trials there are per block. Optseq will then generate a series of schedules that randomize the order of the ITI's and the stimuli in order to find the maximum design efficiency.
Using the IAPS photos example above, let us also assume that there are: 1) 160 time points in the experiment; 2) a TR of 2 seconds; 3) A post-stimulus window of 20 seconds to capture the hemodynamic response; 3) Jitters ranging from 2 to 8 seconds; and 4) The three conditions mentioned above, each last 2 seconds per trial, and with 20 instances of DisgustingPic, 15 instances of AttractivePic, and 30 instances of NeutralPic. Furthermore, let us say that we wish to keep the top three schedules generated by optseq, each prefixed by the word IAPS, and that we want to randomly generate 1000 schedules.
Lastly, let us say that we are interested in a specific contrast - for example, calculating the difference in activation between the conditions disgustingPic and attractivePic.
In order to do this, we would type the following:
optseq2 --ntp 160 --tr 2 --psdwin 0 20 2 --ev disgustingPic 2 20 --ev attractivePic 2 15 --ev neutalPic 2 30 --evc 1 -1 0 --nkeep 3 --o IAPS --tnullmin 2 --tnullmax 8 --nsearch 1000
This will generate stimuli presentation schedules and only keep the top three; examples of these schedules, as well as an overview of how the efficiencies are calculated, can be seen in the video.
Chapter 4: The Reckoning - Comparison of optseq to 1d_tool.py
Optseq is a great tool for generating templates for stimuli presentation. However, if only one schedule is generated and applied to all blocks and all subjects, there is the potential for ordering effects to be confounded with your design, however minimal that possibility may be. If optseq is used, I recommend that a unique schedule be generated for each block, and then counterbalance or randomize those blocks across subjects. Furthermore, you may also want to consider randomly sampling the stimuli and ITI's and simulate several runs of your experiment, and then run them through AFNI's 1d_tool.py in order to see how efficient they are. With a working knowledge of optseq and 1d_tool.py, in addition to a steady diet of HotPockets slathered with Nutella, you shall soon become invincible.
You shall be...Perfect.
Optseq, a tool developed by the good people over at MGH, helps the user order the presentation of experimental conditions or stimuli in order to optimize the estimation of beta weights for a given condition or a given contrast. By providing a list of the experimental conditions, the length of the experiment, the TR, and how long and how frequent the experimental conditions last, optseq will generate schedules of stimuli presentation that maximizes the power of the design, both through reducing variance due to noise and increasing the efficiency of estimating beta weights. This is especially important in event-related designs, which are discussed in greater detail below.
Chapter 1: Slow Event-Related Designs
Slow event-related designs refer to experimental paradigms in which the hemodynamic response function (HRF) for a given condition does not overlap with another condition's HRF. For example, let us say that we have an experiment in which IAPS photos are presented to the subject at certain intervals. Let us also say that there are three classes of photos (or conditions): 1) Disgusting pictures (DisgustingPic); 2) Attractive pictures (AttractivePic); and neutral pictures (NeutralPic). The order in which these pictures are presented will be at a long enough time interval so that the HRFs do not overlap, as shown in the following figure (Note: All of the following figures are taken from the AFNI website; all credit and honor is theirs. They may find these later and try to sue me, but that is a risk I am willing to take):
The interstimulus time interval (ITI) in this example is 15 seconds, allowing enough time for the entire HRF to rise and decay, and therefore allow the experimenter to estimate a beta weight for each condition individually without worrying about overlap in the HRFs. (The typical duration of an HRF, from onset to decay back to baseline, is roughly 12 seconds, with a long period of undershoot and recovery thereafter). However, slow event-related designs suffer from relatively long experimental durations, since the time after each stimulus presentation has to allow enough time for the HRF to decay to baseline levels of activity. Furthermore, the subject may become bored after such lengthy "null" periods, and may develop strategies (aka, "sets") when the timing is too predictable. Therefore, quicker stimulus presentation is desirable, even if it leads to overlap in the conditions's HRFs.
Chapter 2: Rapid (or Fast) Event-Related Designs
Rapid event-related designs refer to experimental paradigms in which the ISI between conditions is short enough so that the hemodynamic response function (HRF) for a given condition overlaps with another condition's HRF. Theoretically, given the assumption of linearity of overlapping HRFs, this shouldn't be a problem, and the contribution of each condition's HRF can be determined through a process known as deconvolution. However, this can be an issue when the ISI's are fixed and the presentation of stimuli is fixed as well:
In this example, each condition follows the other in a fixed pattern: A followed by B followed by C. However, the resulting signal arising from the combination of HRFs (shown in purple in the bottom graph) is impossible to disentangle; we have no way of knowing, at any given time point, what amount of the signal is due to condition A, B, or C. In order to resolve this, we must randomize the presentation of the stimuli and also the duration of the ISI's (a process known as "jittering"):
Chapter 3: Optseq
In order to use optseq, first download the software from the MGH website (or, just google "optseq" and click on the first hit that comes up). Put the shell script into a folder somewhere in your path (such as ~/abin, if you have already downloaded AFNI) so that it will execute from anywhere within the shell. After you have done this you may also want to type "rehash" at the command line in order to update the paths. Then, type "optseq2" to test whether the program executes or not (if it does, you should get the help output, which is generated when no argument are given).
Optseq needs four pieces of information: 1) The number of time points in a block of your experiment; 2) The TR; 3) A permissible range of the minimum and maximum amounts of time after presentation of a stimulus and the start of the next (aka, the post-stimulus delay, or PSD); and 4) How many conditions there are in your experiment, as well as how long they are per trial and how many trials there are per block. Optseq will then generate a series of schedules that randomize the order of the ITI's and the stimuli in order to find the maximum design efficiency.
Using the IAPS photos example above, let us also assume that there are: 1) 160 time points in the experiment; 2) a TR of 2 seconds; 3) A post-stimulus window of 20 seconds to capture the hemodynamic response; 3) Jitters ranging from 2 to 8 seconds; and 4) The three conditions mentioned above, each last 2 seconds per trial, and with 20 instances of DisgustingPic, 15 instances of AttractivePic, and 30 instances of NeutralPic. Furthermore, let us say that we wish to keep the top three schedules generated by optseq, each prefixed by the word IAPS, and that we want to randomly generate 1000 schedules.
Lastly, let us say that we are interested in a specific contrast - for example, calculating the difference in activation between the conditions disgustingPic and attractivePic.
In order to do this, we would type the following:
optseq2 --ntp 160 --tr 2 --psdwin 0 20 2 --ev disgustingPic 2 20 --ev attractivePic 2 15 --ev neutalPic 2 30 --evc 1 -1 0 --nkeep 3 --o IAPS --tnullmin 2 --tnullmax 8 --nsearch 1000
This will generate stimuli presentation schedules and only keep the top three; examples of these schedules, as well as an overview of how the efficiencies are calculated, can be seen in the video.
Chapter 4: The Reckoning - Comparison of optseq to 1d_tool.py
Optseq is a great tool for generating templates for stimuli presentation. However, if only one schedule is generated and applied to all blocks and all subjects, there is the potential for ordering effects to be confounded with your design, however minimal that possibility may be. If optseq is used, I recommend that a unique schedule be generated for each block, and then counterbalance or randomize those blocks across subjects. Furthermore, you may also want to consider randomly sampling the stimuli and ITI's and simulate several runs of your experiment, and then run them through AFNI's 1d_tool.py in order to see how efficient they are. With a working knowledge of optseq and 1d_tool.py, in addition to a steady diet of HotPockets slathered with Nutella, you shall soon become invincible.
You shall be...Perfect.