So far we have covered functional connectivity analysis with resting-state datasets. These analyses focus on the overall timecourse of BOLD activity for a person who is at rest, with the assumption that random fluctuations in the BOLD response that are correlated implies some sort of communication happening between them. Whether or not this assumption is true, and whether or not flying lobsters from Mars descend to Earth every night and play Scrabble on top of the Chrysler Building, is still a matter of intense debate.
However, the majority of studies are not resting-state experiments, but instead have participants perform a wide variety of interesting tasks, such as estimating how much a luxury car costs while surrounded by supermodels. If the participant is close enough to the actual price without going over, then he -
No, wait! Sorry, I was describing The Price is Right. The actual things participants do in FMRI experiments are much more bizarre, involving tasks such as listening to whales mate with each other*, or learning associations between receiving painful electrical shocks and pictures of different-colored shades of earwax.
In any case, these studies can attempt to ask the same questions raised by resting-state experiments: Whether there is any sort of functional correlation between different voxels within different conditions. However, traditional analyses which average beta estimates across all trials in a condition cannot answer this, since any variance in that condition is lost after averaging all of the individual betas together.
Beta series analysis (Rissman, Gazzaley, & D'Esposito, 2004), on the other hand, is interested in the trial-by-trial variability for each condition, under the assumption that voxels which show a similar pattern of individual trial estimates over time are interacting with each other. This is the same concept that we used for correlating timecourses of BOLD activity while a participant was at rest; all we are doing now is applying it to statistical maps where the timecourse is instead a concatenated series of betas.

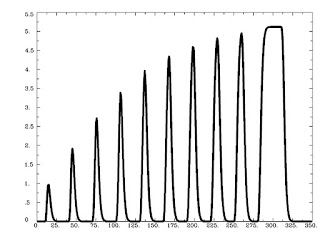
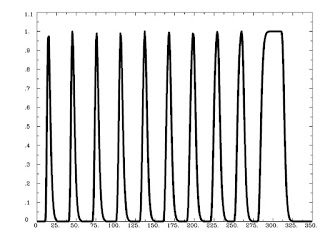
Figure 1 from Rissman et al (2004). The caption is mostly self-explanatory, but note that for the beta-series correlation, we are looking at the amplitude estimates, or peaks of each waveform for each condition in each trial. Therefore, we would starting stringing together betas for each condition, and the resulting timecourse for, say, the Cue condition would be similar to drawing a line between the peaks of the first waveform in each trial (the greenish-looking ones).
The first step to do this is to put each individual trial into your model; which, mercifully, is easy to do with AFNI. Instead of using the -stim_times option that one normally uses, instead use -stim_times_IM, which will generate a beta for each individual trial for that condition. A similar process can be done in SPM and FSL, but as far as I know, each trial has to be coded and entered separately, which can take a long time; there are ways to code around this, but they are more complicated.
Assuming that you have run your 3dDeconvolve script with the -stim_times_IM option, however, you should now have each individual beta for that condition output into your statistics dataset. The last preparation step is to extract them with a backhoe, or - if you have somehow lost yours - with a tool such as 3dbucket, which can easily extract the necessary beta weights (Here I am focusing on beta weights for trials where participants made a button press with their left hand; modify this to reflect which condition you are interested in):
3dbucket -prefix Left_Betas stats.s204+tlrc'[15..69(2)]'
As a reminder, the quotations and brackets mean to do a sub-brik selection; the ellipses mean to take those sub-briks between the boundaries specified; and the 2 in parentheses means to extract every other beta weight, since these statistics are interleaved with T-statistics, which we will want to avoid.
Tomorrow we will finish up how to do this for a single subject. (It's not too late to turn back!)
*Fensterwhacker, D. T. (2011). A Whale of a Night: An Investigation into the Neural Correlates of Listening to Whales Mating.
Journal of Mongolian Neuropsychiatry, 2, 113-120.